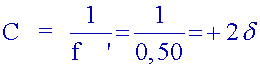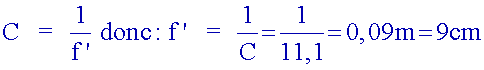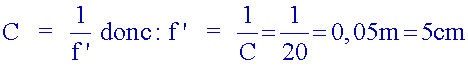Formation des
images
optiques
1. Les
conditions pour qu’un objet soit vu…
1.2 L’objet
doit émettre de la lumière
Une source lumineuse émet
de la
lumière
Une
source lumineuse « primaire » produit de la lumière
(
ex : soleil,
lampe)
Etude
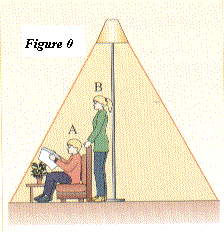
la figure :
A quelle condition Arthur peut-il lire
son
journal ?
Arthur ne peut lire son journal que si
le lampadaire est allumé.
Le
journal étant opaque ( et non poli), il diffuse la
lumière qu’il
reçoit : 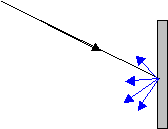
Une
source lumineuse « secondaire » est un objet éclairé qui renvoie la
lumière provenant d’une autre source
On ne peut
voir un objet que s'il émet de la lumière ou s'il est éclairé
1.3 Propagation
de la lumière
Comment
appelle-t-on les milieux dans lesquels la lumière se propage ?
ce sont des
milieux transparents
Expérience
avec le laser :
Une source laser est allumée. On ne peut voir le faisceau lumineux que
si on soupoudre de la poussière de craie ( qui diffuse la lumière). Le
faisceau lumineux est une ligne droite.
Dans
un milieu transparent et homogène, la lumière se propage en ligne
droite.
On représente le trajet de la
lumière par un rayon
lumineux ( sur lequel on place une flèche !)
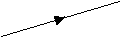
(
un faisceau lumineux est un ensemble de rayons lumineux)
1.4 Pourquoi
voit-on ?
Etude
la figure 1 :
Si le lampadaire est allumé, pourquoi
Arthur et
Brigitte peuvent-ils lire le journal ?
La lumière reçue par le journal est
renvoyée dans la
direction d’Arthur et dans celle de Brigitte.
Représenter
le trajet suivi par la lumière….
Pourquoi Arthur
ne voit-il pas le lampadaire ni le pot de fleurs posé sur la
table ?
Arthur ne voit ni le lampadaire ni le
pot de fleurs
car la lumière provenant de ces deux objets ne pénètre pas dans ses yeux
Un objet, lumineux ou éclairé, n'est
visible que si la lumière
qu’il envoie pénètre dans l'oeil de l'observateur
1.5 L’œil,
vu par la physique…
1 :
cornée
2 :
humeur aqueuse
3 :
iris
4 :
cristallin
5 :
rétine
6 :
nerf optique
7 :
humeur vitrée
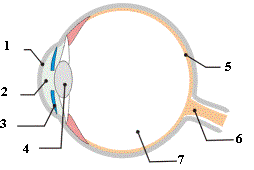
Pour
le physicien, l’œil est
constitué de trois parties principales :
- L’ensemble
pupille-iris qui joue le rôle de diaphragme
(ouverture circulaire de
diamètre variable) ;
- Le cristallin qui
joue le rôle de lentille ;
- La
rétine qui joue le rôle d’écran
2. Les
lentilles : observations
2.1 Qu’est-ce
qu’une lentille ?
Une lentille est un milieu
transparent limité par deux
surfaces dont l'une au moins n’est pas plane.
2.2 Différentes
formes de lentilles
| Lentille |
Bords
minces |
Bords
épais |
| Schémas |
 |
 |
| Symbole |
 |
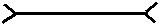 |
2.3 Action
sur un faisceau parallèle
1) Lentilles
à bords minces
Le faisceau émergent converge
en un point 
( plus la lentille est bombée, plus
elle est convergente
Une lentille à bords mince est une
lentille convergente
2) Lentilles
à bords épais
Le faisceau émergent diverge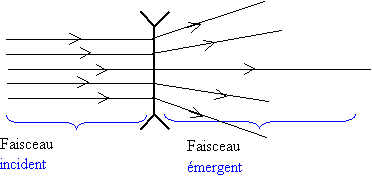
Une
lentille à bords épais est une
lentille divergente
2.5 Observation
d’un texte
Observer successivement un mot de
ce document au travers
des lentilles marquées +3 et –3. Comparer les tailles des images
obtenues à
celle de l’objet.
Une lentille convergente a un effet
de grossissement des
objets (loupe).
Une lentille divergente a un effet
de réduction des objets.
Compléter les schémas ci-dessous en
représentant ce que l’on voit au travers des lentilles.

Le
cristallin étant une lentille convergente, nous étudierons seulement
les
lentilles de ce type.
3. LES POINTS IMPORTANTS D’UNE LENTILLE CONVERGENTE
En général, une lentille dévie les rayons lumineux qui la traversent (
à cause du phénomène de réfraction).
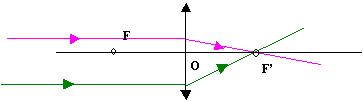
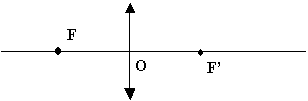
3.1 Centre optique
Pour une lentille mince, la partie centrale est assimilée à un point
appelé centre
optique O.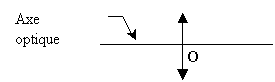
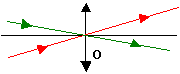
Faire passer un rayon lumineux par le centre de la lentille .
Qu’observe-t-on?
Le rayon n'est pas dévié
Tout
rayon incident qui passe par le centre optique d’une lentille mince
n'est pas dévié
3.2 Foyer image
On envoie un faisceau parallèle à l’axe optique sur la lentille.
Que constate-t-on pour le faisceau
émergent? 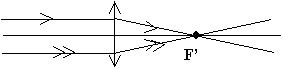
Le faisceau émergent converge en un
point que l'on appelle foyer
image F '.
Tout
rayon incident parallèle à l'axe optique, ressort en passant par le
foyer image F '
3. 3 Foyer objet
On déplace la lentille de façon que le faisceau émergent soit parallèle
à l’axe optique.
Que constate-t-on pour le faisceau
incident ?
Le faisceau incident provient d'un
point que l'on appelle foyer
objet F.
Tout rayon incident passant par
le foyer objet F de la lentille,
ressort parallèlement à l’axe optique
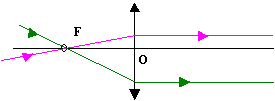
Remarque
importante : F et F’ sont symétriques par
rapport à la lentille ( FO= OF ' )
4. DISTANCE FOCALE F’ ; VERGENCE
4.1 Distance focale
On appelle distance focale, la distance du centre de la lentille au
foyer image, on la note f ’.
Cette grandeur caractérise les lentilles ; elle s’exprime en mètre ( le
plus souvent en cm) .
4.2 Expérience
On utilisera comme source lumineuse le plafonnier de la salle de cours,
une lentille convergente ( notée +11,1 δ ) et comme écran, une
table placée
exactement sous le plafonnier.
Le plafonnier est éloigné de la table.
Comment peut-on considérer les
rayons venant du plafonnier ?
Le plafonnier est loin de la lentille.
On peut considérer que les rayons sont parallèles entre eux.
Placer la lentille perpendiculairement
à la direction de ces rayons
lumineux. Déplacer la lentille par rapport à la table. Observer la
tache lumineuse recueillie sur la table.
Lorsque l’image est la plus
petite possible, mesurer à l’aide d’une règle la distance
table-lentille.
d ≈ 9 cm
Recommencer avec une lentille notée
+20 δ; d'après
le toucher, cette lentille est-elle plus ou moins convergente que la
précédente?
d ≈ 5 cm ; cette lentille est plus
bombée que la précédente, donc plus convergente.
Plus la distance focale est petite,
plus la lentille fait converger
les rayons
Remarque :
la distance focale d’une lentille
convergente est positive.
la
distance focale d’une lentille divergente est négative
4.3 Vergence C d’une lentille
 avec f ’ en
m
C en dioptries
( δ
)
avec f ’ en
m
C en dioptries
( δ
) 
Plus la vergence est grande,
plus la lentille fait converger les rayons
Remarque : la
vergence d’une lentille convergente
est positive.
la vergence d’une lentille divergente
est négative
1. Calculer
la vergence d’une lentille dont la
distance focale
est f’ = 0,50m.
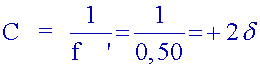
2. Calculer
la distance focale d’une lentille dont la vergence est C = 11,1 δ
Calculer
la distance focale d’une lentille dont la vergence est C = 20 δ
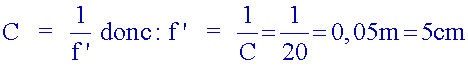
3.
Calculer la vergence d’une lentille dont la distance focale
est f’ = 25cm
il
faut d'abord convertir la distance focale en m! 25
cm = 0,25 m

5. CAS D’UN OBJET SITUE A DIFFERENTES
DISTANCES DE LA LENTILLE
5.1 Etude expérimentale
a) Mesures :
On utilise cette fois le banc d’optique avec une lettre F de hauteur
égale à cm comme
objet noté AB, une lentille convergente de 3,3δ et
un écran.
Pour différentes positions lentille-objet, on détermine la nature, la
taille et la position de l’image A’B’.
On notera OA la position de l’objet par rapport à la lentille et OA’ la
position de l’image par rapport à la lentille.
| OA (cm) |
OA’(cm) |
A’B’(cm) |
Sens de
l’image |
Nature de l’image |
| 100 |
43 |
|
renversée |
réelle |
| 70 |
52 |
|
renversée |
réelle |
| 50 |
77 |
|
renversée |
réelle |
L'image est réelle car elle
se forme sur l'écran
Que constate-t-on quand on rapproche
la lentille de l’objet
?
L'image s'éloigne de la lentille et
elle devient de plus en plus grande
On s’intéresse maintenant à la
position objet-lentille OA égale à 30cm.
Où se trouve alors l’image ?
L’image se trouve alors à une distance
très éloignée de la lentille
(visible sur le mur de la salle suivant la disposition des bancs
d’optique), on la considérera à l’infini.
Même question lorsque la position
objet-lentille vaut 16cm.
On ne peut pas recueillir d’image sur
un écran, celle-ci est alors
virtuelle.
(loupe)
b ) Conclusion :
Lorsque l’objet est situé entre l’infini et le foyer objet
F, on obtient toujours une image réelle mais renversée,
plus
grande ou plus petite que l’objet (suivant la position OA).
Par contre, lorsque l’objet se situe entre F et O, on obtient une image
virtuelle.
5.2 Construction graphique d’une
image
L’objet AB est représenté par une flèche. A étant sur l’axe optique,
son image A’ est également sur l’axe optique.
Tous les rayons issus de B ( objet ) se coupent en B’ ( image de B par
la lentille) ; parmi tous les rayons, on en trace 3 qui ont des
propriétés simples .
Tracer les 3 rayons issus de B qui permettent de déterminer B’.
correction

















 avec f ’ en
m
C en dioptries
( δ
)
avec f ’ en
m
C en dioptries
( δ
)