Ph 2.4 La mesure du temps
4. Le
Pendule
4.1 Qu’est-ce qu’un pendule ?
Un pendule est un petit objet suspendu à un fil . (La
taille de l’objet est petite comparée à la longueur du
fil).
longueur du
fil).
En pratique on prendra une boule de laiton, de bois … de
masse m
A l’équilibre, le pendule est vertical
Quand on l’écarte de sa position d’équilibre, il oscille
de part et d’autre de la verticale.
4.2 La période du pendule
Une oscillation : un aller et retour
La
période
du pendule est le temps mis pour faire une oscillation.
4.3 Etude expérimentale
On veut trouver l’expression de la période du pendule.
La période étant petite, on va mesurer le temps mis pour
effectuer 20 oscillations et en déduire la période.
1 ) De quels paramètres peut dépendre-à priori- la période du
pendule ?
- De sa masse
- De la longueur
l
- De l’angle
α dont
on l’écarte par rapport à la verticale ( appelé amplitude ).
On mesure
cet
angle grâce à un rapporteur.
2) Manipulations
a )Influence de l’amplitude
Prendre un pendule en laiton. Régler la longueur l
= 60 cm.
L’écarter d’un
angle α par rapport à la verticale. Mesurer T
.
| α (°) |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
| T(s) |
1,5 |
1,5 |
1,5 |
1,5 |
1,5 |
1,6 |
1,6 |
1,6 |
Conclusion :
La période ne dépend pas
de l'amplitude ( tant qu'elle est petite α
< 20°)
b ) Influence de la masse
Prendre un pendule en laiton de longueur l
= 60 cm
L’écarter d’un angle α
= 20° par rapport à la verticale.
Mesurer T.
Recommencer avec le pendule en bois
|
bois |
laiton |
| m(g) |
12,5 |
34,5 |
| T(s) |
1,6 |
1,6 |
Conclusion :
Aux erreurs expérimentales près, la
période ne dépend pas de la masse du pendule.
c ) Influence de la longueur
Prendre un pendule en laiton. Régler la longueur l.
L’écarter d’un angle α
= 20° par rapport à la verticale. Mesurer T.
| l (m) |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
1,0 |
| T(s) |
0,9 |
1,1 |
1,2
|
1,4 |
1,5 |
1,7 |
1,8 |
2,0 |
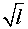 |
0,44 |
|
0,63 |
|
|
|
|
|
Conclusion :
La période du pendule dépend de la
longueur l.
Quand l
augmente, T augmente. ( mais T n'est pas proportionnelle à l.
3) Approfondissement
On propose les expressions suivantes de la période :
A partir des résultats obtenus précédemment, quelle(s) expression( s)
de la période doit-on éliminer ?Justifier.
La période ne dépend pas de
m ; il faut éliminer les expressions 1 et 3.
La période ne dépend pas de α ; il faut éliminer l'
expression 5.
La période augmente quand l
augmente; il faut éliminer l'expression 2 .
Il reste l'expression 4.
Dans le tableau §2.c
calculer pour chacune des mesures 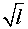 .
.
Tracer T en fonction
de 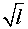
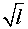
 longueur du
fil).
longueur du
fil).
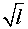
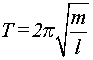
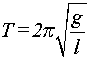

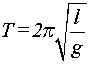

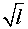 .
.