Le ballon est soumis à son poids
 (on considère que la poussée d'Archimède et les frottements
sont négligeables ....)
(on considère que la poussée d'Archimède et les frottements
sont négligeables ....)On applique la seconde loi de Newton :
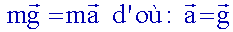
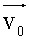 faisant
un angle α
avec l’horizontale.
faisant
un angle α
avec l’horizontale.

Tracer la courbe vx(t)
en « nuage de
points ».
Ajouter une courbe de tendance .
Faire écrire l’équation de la courbe de tendance ;
l’écriture proposée vous semble-t-elle correcte ? Rectifier le
cas
échéant.
Même travail pour vy(t)

Vx(t) est une
fonction affine à peu
près constante.
Vy(t) est une fonction affine décroissante
Tracer la courbe y(x).

La courbe est une parabole.
Retrouver, par une étude physique complète, les expressions vx(t) et vy(t) ;
On se place dans le référentiel terrestre, galiléen.
Le ballon est soumis à son poids  (on considère que la poussée d'Archimède et les frottements
sont négligeables ....)
(on considère que la poussée d'Archimède et les frottements
sont négligeables ....)
On applique la seconde loi de Newton
:
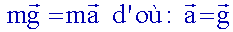
On projette sur les axes :

ax
= 0 et ay= - g
On calcule la vitesse :
Vx
(t) = k1
or, à t =
0, Vx
(0) =
k1= V0x
donc
Vx
(t) = V0x
Vy (t) = - g × t + k2
or, à t =
0, Vy(0)= k2 = V0y
donc
Vy (t) = - g × t
+ V0y
Les allures des courbes sont-elles conformes à la théorie?
La courbe Vx(t)
est
sensiblement constante; cela correspond à l'équation:
Vx
(t) =
V0x
Vy(t) est une fonction affine décroissante;
cela
corrrespond à l'équation:
Vy
(t) = -
g t
+ V0y
Quelles sont les valeurs mesurées de ax(t) et ay(t) ?
Le tableur indique :
Vx(t) = 0,091 t + 1,814 donc ax(t)
= 0,091 m.s-2
Vy(t) = - 10,154 t + 3,524 donc
ay(t) = - 10,154 m.s-2
Comparer aux valeurs théoriques. Comment interprétez-vous les écarts éventuels ?
En théorie ax(t) = 0 et ay(t) = -9,8 m.s-2; les valeurs sont assez proches, les écarts s'expliquent par les erreurs de pointage...
Exprimez Vx(0) et Vy(0). En déduire V0
Vx(t) = 0,091 t +
1,81 donc : Vx(0)
= V0x = 1,8 m.s-1
Vy(t) = - 10,154 t + 3,524 donc : Vy(0)
= V0y = 3,52 m.s-1
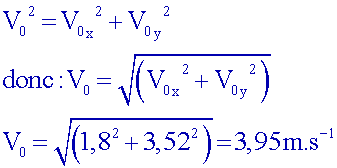
Trouver la valeur de α
Vx(0) = 1,8 m.s-1
= V0×cos α
Vy(0) = 3,524 m.s-1
= V0×sin α
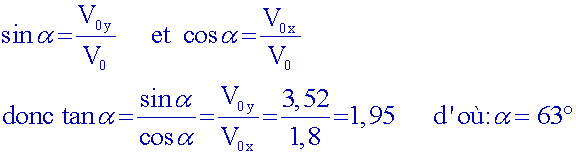
Faire calculer x(t) et y(t) pour cette valeur de α
On a : Vx
(t) = V0×cos α
donc : x(t) = V0×cos
α × t + k3
pour déterminer k3
: x(0) = V0×cos
α × 0 + k3=
0 donc : k3=
0
et : x(t) = V0×cos α × t
De même : Vy (t)
= - g t
+ V0×sin α
donc : y(t) = - 1/2 g t² + V0×sin
α × t
+ k4
pour déterminer k4
: y(0) = - 1/2 g × 0 + V0×sin
α × 0 + k4=
0 donc : k4=
0
et : y(t) =
- 1/2 g t² + V0×sin
α × t
Rentrer les expressions dans le tableur et faire calculer x(t) et y(t)
pour α = 80°
Superposer la nouvelle trajectoire
avec la précédente.

Même travail que précédemment.
Quelle valeur de α faut-il choisir pour atteindre un objectif éloigné ?
Pour atteindre un objectif éloigné, il est préférable de choisir α = 45°