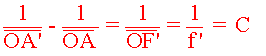LENTILLES
MINCES CONVERGENTES
1.
Définitions :
1.1.
Rayons lumineux
 Dans un
milieu transparent et homogène, la lumière se
propage en ligne droite : rayon lumineux
Dans un
milieu transparent et homogène, la lumière se
propage en ligne droite : rayon lumineux
Remarque : un rayon lumineux est
représenté par un segment de droite
orienté.
Un
rayon qui arrive
sur un système optique est un rayon
incident
Un rayon qui sort
d’ un
système optique est un rayon émergent
1.2.
Objets et images
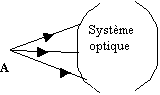
1) Le point objet est l’intersection des rayons
incidents
| Objet
réel |
Objet virtuel |
|
|
|
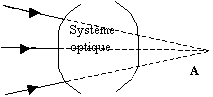
Cas particulier
d’un
objet ( réel ) situé à
l’infini : les rayons incidents sont
parallèles
entre eux.

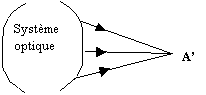
2) Le point image est l’intersection des
rayons
émergents
|
Image
réelle
|
Image
virtuelle
|
|
|
|
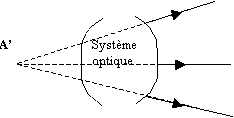
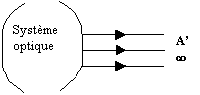
Cas particulier
d’une image ( réelle ) située
à l’infini :
les rayons
émergents sont parallèles
entre eux.
1.3.
Lentilles
Une lentille est un milieu transparent limité par deux
surfaces dont l'une au moins n’est pas plane.
Une lentille est
« mince » quand
l’épaisseur est négligeable
devant le
rayon de courbure.
Prendre
une lentille à bords minces ;
la placer sur le trajet d’un faisceau parallèle.
Qu’observe-t-on?
Le
faisceau de
lumière converge
Recommencer
avec une lentille à bords épais.
Le faisceau de lumière diverge
Caractériser
chacune des lentilles.
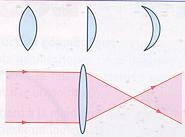
La lentille à
bords minces est une lentille convergente.
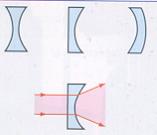
La
lentille à bords épais est une lentille divergente.
|
Lentille
convergente
|
Lentille
divergente
|
|
|
|
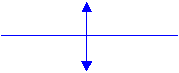
Symbole
d’une lentille mince
convergente:
2.
propriétés des lentilles
En
général, une lentille dévie les rayons
lumineux qui la traversent .
2.1
Points
importants
1) Centre optique
Pour
une lentille mince,
la partie centrale est assimilée à un point
appelé centre
optique O.
Faire
passer un rayon lumineux par le centre de la lentille .
Qu’observe-t-on?
Le rayon n’est pas
dévié
Tout rayon incident
qui passe par le centre optique d’une
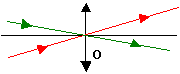
lentille mince n’est pas dévié
2) Foyers principaux
a. Foyer principal objet
Déplacer
la lentille de façon que le faisceau émergent
soit parallèle à l’axe optique.
Que
constate-ton pour le faisceau incident?
Tous
les rayons se coupent en un point F
Mesurer
alors la distance entre la source lumineuse et la lentille.
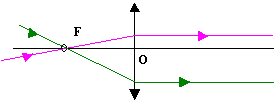
Tout rayon incident passant par
le foyer principal objet F de la lentille,
ressort parallèlement à l’axe optique
b.Foyer
principal image
Placer
la lentille loin de la source lumineuse.
Comment est alors le faisceau incident?
parallèle
à l'axe optique
Que
constate-t-on pour le faisceau émergent?
Tous les rayons se coupent
en un point F'
v
Mesurer
alors la distance entre la
lentille et le point d’intersection des rayons lumineux.
Tout
rayon incident
parallèle à l’axe optique, ressort en
passant par le foyer principal image
F’ de la lentille.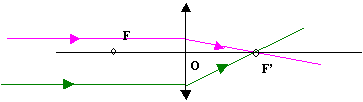
Remarque
importante : F et F’ sont symétriques par
rapport à la lentille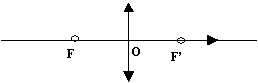
2.2.
Distance focale f’ ; vergence
1) Distance focale
Par
convention, on oriente
l’axe optique dans le sens de propagation de la
lumière et on choisit pour origine le centre optique O.
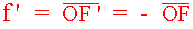 avec
avec  ( pour une lentille convergente )
( pour une lentille convergente )
Plus la distance focale
est petite,
plus la lentille fait converger les rayons
2)Vergence
C d’une lentille
 avec f ’ en
m C en dioptries ( δ
)
avec f ’ en
m C en dioptries ( δ
)
Plus la vergence est grande,
plus la lentille fait converger les rayons
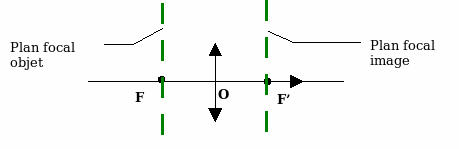
2.3
Plans
focaux
Ce sont les
plans
perpendiculaires à l’axe optique et qui
contiennent les foyers principaux
3. Applications
3.1.Construction graphique de
l’image d’un point objet B non
situé sur l’axe principal :
Tous les rayons issus de B
( objet ) se coupent en B’ ( image de B par la
lentille) ; parmi tous les rayons, on en trace 3 qui ont des
propriétés simples .
Tracer les
3
rayons issus de B qui permettent de déterminer B’.
Méthode
( lien ) 
3.2.Marche
d’un faisceau lumineux issu
de S et couvrant la lentille :
Tracer la
marche
du faisceau lumineux issu de B qui couvre la lentille.

Méthode
( lien )
3.3.
Construction d’un objet
connaissant l’image
Trouver
l’objet B connaissant son image B’ :
Méthode
( lien )
3.4.Image
d’un objet à l’infini non
situé sur l’axe
Méthode
( lien )
4.Images
formées par une lentille mince convergente
4.1.
Constructions
géométriques
Donnée :
Si un objet AB est perpendiculaire à l’axe
optique, son image A’B’ est également
perpendiculaire à l’axe optique.
Trouver
l’image A’B’ de AB dans chacun des cas et
indiquer les caractéristiques de
l’image ( réelle, virtuelle, droite,
renversée, agrandie
Correction
4.2 Approche
expérimentale
1)Première
approche
Sur
le banc d'optique, placer l’objet (diapositive) à
une extrémité et l’écran
à l’autre.
Déplacer la
lentille vers
l’écran afin d’obtenir sur
l’écran l’image nette de
l’objet.
Combien
d’images nettes peut-on
obtenir ?
On
obtient 2 images
Comparer dans
chaque cas la taille de
l’image à celle de l’objet ; quel
cas
correspond à un appareil photo ?
lorsque la lentille
est éloignée de l’objet ( AO > 2
f ’)
quel
cas
correspond à un projecteur de diapos ?
lorsque
la lentille
est proche de l’objet (
2f ’>AO>f ’)
2)Mesure
approchée de la distance focale d’une lentille
convergente :
Se placer dans le cas
où l’image est plus grande que l’objet.
Quelle
est la
position de l’image ? (une
distance de plus
d’un mètre correspond pratiquement, en optique,
à une distance infinie).
La
distance
OA’> 1m, on peut considérer que
l’image est à l’infini.
Quelle est
alors la position de l’objet ?
L’objet est
donc dans le plan focal de la lentille.
Quelle
est la
mesure de la distance focale ?
f ' = OA’=
………
Comparer
à l’indication portée sur la lentille.
3)Evolution
de
l’image
L’objet
reste fixe ; déplacer la lentille pour se placer
dans chacun des cas ci-dessous ; déplacer
l’écran pour obtenir une image nette.
Donner les caractéristiques de cette image (nature, sens et
taille…)
On obtient
les mêmes résultats que dans la construction
graphique
4.3.
Formules de
conjugaison et de grandissement
1) Manipulation
2)Résultats
expérimentaux
Comparer
le résultat de la
5ème colonne avec la valeur de
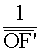
. Quelle
relation peut-on
écrire ?.
Les
résultats sont égaux aux erreurs de mesure
près.
Comparer
le résultat des
6ème et 7ème
colonnes. Conclure.
Les
résultats sont égaux aux erreurs de mesure
près.
3)Relations
de
conjugaison
|
formule
de
conjugaison
|
grandissement
|
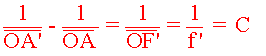 |
 |
4.4.
Conditions
de Gauss
1)Etude
expérimentale
Positionner la
lentille et former une image nette sur
l’écran. Faire pivoter
légèrement la lentille autour de son
axe ; que constate-t-on pour l’image ?
L’image
devient floue
Placer un
diaphragme devant la lentille et le fermer progressivement. Que
constate-t-on pour l’image ?
L’image
gagne en netteté mais perd de la luminosité.
2)Conclusions
Quelles sont les
conditions d’obtention d’images nettes ?
Conditions
de
Gauss
- L’objet doit
être petit et situé au voisinage de
l’axe optique ; les rayons sont alors peu
inclinés par rapport à l’axe optique (
« rayons paraxiaux » ).
- La
lentille doit
être diaphragmée ( les rayons incidents passent au
voisinage du centre optique )


 Dans un
milieu transparent et homogène, la lumière se
propage en ligne droite : rayon lumineux
Dans un
milieu transparent et homogène, la lumière se
propage en ligne droite : rayon lumineux




 lentille mince n’est pas dévié
lentille mince n’est pas dévié


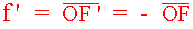 avec
avec  ( pour une lentille convergente )
( pour une lentille convergente ) avec f ’ en
m C en dioptries ( δ
)
avec f ’ en
m C en dioptries ( δ
)




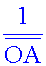
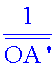
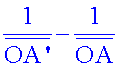

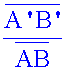
 . Quelle
relation peut-on
écrire ?.
. Quelle
relation peut-on
écrire ?.