| Miroir M1 | Miroir M2 | Miroir M3 | ||||
| Forme au toucher | Plan | Concave | Convexe | |||
| Position de l’objet | Près | Loin | Près | Loin | Près | Loin |
| Caractéristiques de l’image |
droite même grandeur |
droite
même grandeur |
droite
plus grande que l'objet |
renversée plus petite que l'objet |
droite
plus petite que l'objet |
droite
plus petite que l'objet |
Le rayon qui arrive sur le miroir est le rayon incident ; il rencontre le miroir au point d’incidence I.
La droite perpendiculaire au miroir plan en I est la
normale
au miroir.
1ère
loi :
Le rayon réfléchi
est dans le plan d’incidence ( défini par le rayon
incident et la
normale en I )
2ème
loi : L’angle
de réflexion (par rapport à la
normale) est égal à celui d’incidence: i = r

Cas d’un rayon qui arrive perpendiculairement au miroir.
Un rayon qui arrive perpendiculairement au miroir se réfléchit sur lui-même
Construction de l'image d'un objet (correction)
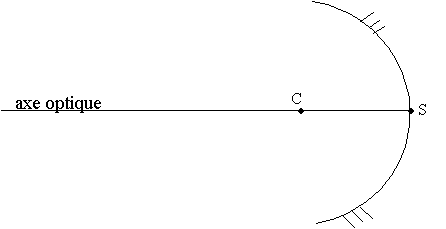
Que dire du rayon réfléchi?
Il
passe par C
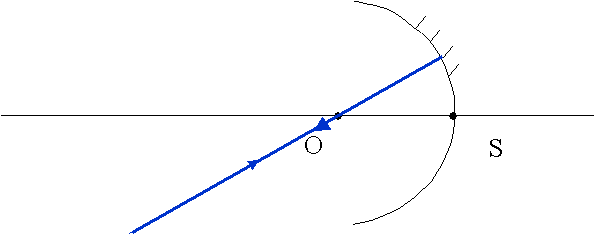
Comment appelle-t-on C ?
C : Centre optique
Tout rayon incident passant par C n'est pas dévié
Tracer 2 rayons parallèles à l’axe
optique et
faiblement
écartés de l’axe optique.
Tracer les rayons réfléchis correspondants.
Vérifier que les rayons réfléchis passent par un
même
point F’.

Donner la définition du foyer image F’du miroir sphérique concave.
Tout rayon incident parallèle à l'axe ressort du miroir en passant par F '
Où est situé F’ dans le segment [SC] ?
F' est au milieu de SC
Un miroir concave est-il divergent ou convergent ?
Un miroir concave est convergent
Proposer un protocole pour déterminer expérimentalement la distance focale du miroir concave mis à votre disposition. Effectuer la mesure (on peut incliner légèrement le miroir de manière à voir l’image se former le cas échéant sur un écran à coté du banc optique)
On place le miroir loin de la source pour
que les
rayons incidents soient parallèles à l'axe.
On fait pivoter légèrement
le miroir et - à l'aide de l'écran - on trouve le point F' où
convergent
les rayons
On mesure CF'
Tracer un rayon incident non parallèle à l’axe optique principal et passant par le foyer F. Que constate-t-on ?
Il ressort parallèle à l'axe optique.

Le
foyer objet F et le foyer image F ' sont confondus. On parle
de foyer F,
milieu de CS
Tout
rayon
passant par F ressort parallèle à l'axe optique et réciproquement.
La
distance focale : f = f ' = CS/2 = R/2
Envoyer des rayons très inclinés par rapport à l'ae optique du miroir. Qu’observe-t-on ?
Ils ne sont pas
réfléchis en passant par F
Envoyer des rayons parallèles à l’axe ; qu’observe-t-on pour les rayons extrêmes ?
Ils ne sont pas réfléchis en passant par F
En déduire les conditions de Gauss pour les miroirs.
Les
rayons incidents doivent être peu inclinés
par rapport à l'axe optique
Ils doivent frapper le miroir au
voisinage de son sommet.

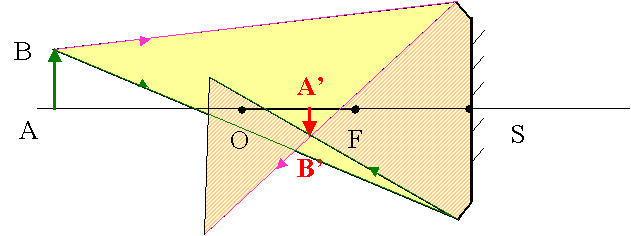
Le rayon lumineux issu de B et parallèle à l’axe optique principal est réfléchi et passe par F.
Le rayon lumineux issu de B et passant par C est réfléchi selon la direction d’incidence.
Le rayon lumineux issu de B et passant par F est réfléchi parallèlement à l’axe optique principal.
Travail demandé :Sur un schéma (échelle 1), dessiner le symbole d’un miroir concave de sommet S et de rayon R = 6 cm. Placer le foyer F et le centre de courbure C. L’objet AB est perpendiculaire à l’axe optique et A est un point de cet axe ( AB = 1,5 cm ).
Pour chacun des cas :
tracer les trois rayons utiles à la construction du
point
B’,
tracer le point B’, puis A’, puis l’image A’B’
noter les caractéristiques de l’image (agrandie ou
rétrécie, droite ou renversée, réelle ou virtuelle ?)
vérifier que ces caractéristiques sont bien en
accord
avec les observations de l’introduction
faire, lorsque c’est possible !- une
vérification
sur le banc d’optique.
Construire la marche d’un faisceau lumineux issu du point B de l’objet couvrant le miroir(cas où SA = 11 cm)
correction