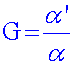Ph 1.5     LA LUNETTE ASTRONOMIQUE

1. Description 

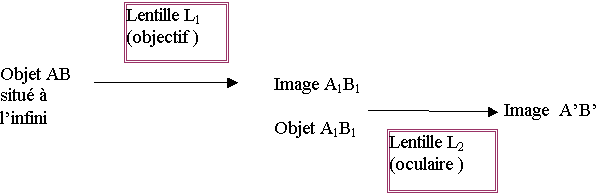
La lunette astronomique est un instrument optique dont le but est d’observer des objets de faible diamètre apparent α
Elle donne de cet objet une image également située à l’infini mais sous un angle apparent α’ que l’on cherche à avoir plus grand que α de façon à :
un peu d'histoire....
A l’origine, instrument militaire, la lunette astronomique révolutionne la science lorsque Galilée a l’idée de la pointer vers le ciel et notamment vers les planètes. Il y fait 3 découvertes majeures par leurs répercussions :
  • la découverte de ce qu’il pense être des mers – en fait ce sont des plaines entre les montagnes mais elles en gardent le nom (mer de la tranquillité par exemple) - sur la lune la fait apparaître non parfaitement ronde,
  • l’observation des phases de Vénus et
  • la découverte de 4 des satellites de Jupiter (Io, Ganymède, Callisto et Europe),
préparent le terrain à la révolution copernicienne : ce n’est plus la Terre qui est au centre du système solaire mais le soleil. Le coup est rude pour les partisans de "l’homme centre du monde".


Une lunette astronomique peut être comparée à 2 tubes coulissant partiellement l’un dans l’autre, chacun possédant à l’une de ses extrémités un système optique constitués de lentilles :

Dans une lunette astronomique, on regarde à la loupe (l’oculaire), l’image agrandie formée par une lentille convergente (l’objectif), d’un objet éloigné.

 

2 Modélisation

Le but de ce TP est de modéliser une lunette astronomique.
 

2.1 Problème posé :

Une lunette astronomique permet de voir une image grossie d’un objet éloigné.
Vous devez simuler une lunette astronomique sur le banc optique en utilisant les deux lentilles à votre disposition:



2.1.1 Etude préalable 

Rappeler les conditions d’observation sans fatigue pour l’œil. 

L’image finale A'B' doit se trouver à l’infini. 
Donc, l’image intermédiaire A1B1 se trouve dans le plan focal objet de L2. 

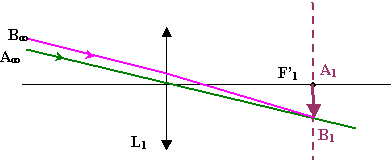
Construire l’image A1B1 donnée par la lentille L1 (objectif) d’un objet AB très éloigné, considéré comme à l’infini.



Où se forme-t-elle ? Est-elle droite ou renversée ?

Elle se forme dans le plan focal image de la lentille. Elle est  renversée et réelle!

   

2.2.2 Choix des lentilles

Quelle est celle des deux lentilles L1 (f1’ = 30 cm) et L2 (f2’ = 5 cm) qui permet d’obtenir l’image intermédiaire la plus grande ?

L’image obtenue est d’autant plus grande que la distance focale est grande.

En déduire la lentille qui sera utilisée en objectif.

La lentille de plus grande distance focale sera utilisée en objectif   (par contre, l’oculaire, utilisé en loupe, grossit d’autant plus que sa distance focale est petite)

 

2.2 Manipulation

L’ojet AB est une mire constituée de traits de 1 mm d’épaisseur et séparés de 1 mm.
En  théorie, elle doit être placée à l’infini.
En pratique, placer les mires sur les paillasses de droite (ou de gauche), le plus loin possible des bancs optiques posés sur les paillasse situées à gauche (ou à droite), à plus de 3,5 m si possible ; alors, les traits ne sont plus visibles, on voit une page grise
Eclairer fortement la mire..  
Placer L1 (f1’ = 30 cm) sur le banc et récupérer l’image intermédiaire A1B1 sur un écran.
Positionner L2 (f2’ = 5 cm) à la place de l’écran, puis éloigner progressivement L2 de A1B1 pour observer une image nette dans L2 utilisée comme loupe.
 

mesurer alors la distance entre L1 et L2 .   Que remarquez-vous ?

 

L’image obtenue est-elle droite ?  agrandie ?

 Elle est renversée. Elle est agrandie 

 

2.3 Construction à l’échelle :

2.3.1 Construction graphique

Représenter le schéma correspondant au montage réalisé (prendre l’échelle 1/5 sur l’axe optique).
Conseils :
L’objet AB étant à l’infini, trouver les caractéristiques de A1B1 (image pour L1)
A’B’ est à l’infini (les rayons émergeants de la lunette sont parallèles) ; où doit se trouver A1B1(objet pour L2) ?

Remarque importante :
A1B1 est dans le plan focal image de L1.
Pour une visison sans effort, A1B1 est dans le plan focal objet de L2.

Le foyer image F’1 de l’objectif est confondu avec le foyer objet F2 de l’oculaire
 
Donc : O1O2 = f ’1 + f ’2  

Pour le système optique complet ( lunette ) l’objet est à l’infini et l’image est également à l’infini ; on dit que la lunette utilisée dans ces conditions est "afocale"

    Construction : voir fichier 1.5 Lunette powerpoint

2.3.2 Calculs

Vérifier les éléments de la construction par le calcul en complétant le tableau suivant :

L1 : objectif L2 : oculaire
Objet : AB Image A1B1 Objet : A1B1 Image A’B’

Position 		L’objet AB est à l’infini
A1 sur F’1

A1 sur F2 A l’infini pour une observation sans fatigue pour l’œil.
Formule de conjugaison à utiliser
Grandeurs algébriques de position
 
Caractéristiques A l’endroit
A l’envers A l’envers Plus grosse que A1B1
A l’envers
 
 

2.4 Grossissement d’une lunette afocale :

Soit α l’angle sous lequel on voit l’objet situé à l'infini sans instrument.
Soit α’ l’angle sous lequel on voit l’objet à travers l’instrument.
 
Faire figurer sur le schéma ces 2 angles.



Le grossissement de la lunette astronomique est donné par la relation :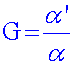     
Exprimer le grossissement de la lunette simulée en fonction des distances focales des lentilles L1 et L2. 

Pour α petit, on peut écrire
pour α’ petit, on peut écrire  

Le grossissement  

Calculer le grossissement de cette lunette.

 La lunette construite a comme grossissement  

Comment pourrait-on améliorer ce grossissement ?

Une lunette grossit d’autant plus que la focale de l’oculaire est petite et/ou d’autant plus que la focale de l’objectif est grande.

Quels sont les inconvénients d’une augmentation de la distance focale de l’objectif ?

Cela augmente la longueur de l’instrument ; de plus, si on augmente la distance focale de l’objectif, on perd en luminosité. 

Quelle autre grandeur caractéristique doit-on prendre en considération pour avoir une lunette de bonne qualité (image suffisamment lumineuse) ?

 Le diamètre de l’objectif ; plus il sera grand, plus lumineuse sera l’image finale. 

Remarque : une lunette portant les nombres (400 × 70) indique un grossissement G = 400 et un diamètre de l’objectif de 70 mm.
 
 

2.5 Position de l’œil : le cercle oculaire.

Rappel : Le cercle oculaire est l’image de l’objectif donnée par l’oculaire.
L’œil doit être placé à son voisinage pour recevoir un maximum de lumière.

Repérer le cercle oculaire : pour cela, orienter la lampe face à la lunette simulée. La lampe doit être placée le plus loin possible. Déplacer l’écran après L2 et repérer la section du faisceau la plus étroite sortant de la lunette.
Noter sa position et son diamètre.

construire le cercle oculaire sur un schéma ( même échelle qu’au § 2.3.1).

 Construction : voir fichier 1.5 Lunette powerpoint