Ph
2.3
Interprétation ondulatoire des modes propres
Prévoir
2 séances !
1.Réflexion d’une onde sur un obstacle
fixe :
1.1Réflexion d’une onde progressive non périodique sur un
obstacle
Une corde élastique est attachée
à un obstacle fixe.
Une petite perturbation est
produite à l’autre extrémité.
Ouvrir le fichier (merci
au collègue!!) et répondre aux questions suivantes :
Que se passe-t-il au niveau de
l’obstacle ?
L’onde
incidente se réfléchit
Quels
sont la direction et le sens de propagation de l’onde
réfléchie ? Quelle est sa vitesse ?
L’onde
réfléchie a la même direction de propagation que l’onde incidente.
Le
sens de propagation est opposé.
Qu’observe-t-on pour la
forme de l’onde réfléchie ?
Si
l’obstacle est fixe : L’onde réfléchie est inversée.
Si
l’obstacle est libre : l’onde réfléchie a la même forme que l’onde
incidente.
1.2 Réflexion d’une onde progressive périodique
sinusoïdale sur un
obstacle:
Ouvrir le fichier
(ondes stationnaires)
et répondre aux questions suivantes :
Qu’observe-t-on pour l’onde
progressive
réfléchie :
L’onde réfléchie
a même
direction de propagation mais sens opposé que l’onde incidente. Elle a
la même période ( donc même fréquence ).
Dans le cas
d’un obstacle fixe ?
elle
est inversée
Dans le cas
d’une extrémité libre ?
elle
a la même forme que
l’onde incidente.
1.3 Onde stationnaire :
1) Superposition de 2 ondes
progressives non périodiques:
Ouvrir le fichier
(
superposition de 2 ébranlements) :
Observer
le mouvement du point sollicité par 2 ondes se propageant en sens
inverse
La déformation
subie par le
point est la somme
des 2 déformations qui se superposent :
obstacle
libre : l’élongation du point a une amplitude supérieure à
celle dûe à une seule onde. obstacle fixe :
l’élongation du point a une amplitude inférieure (voire nulle!), à
celle
dûe à une seule onde.
2) Superposition d’une onde progressive
périodique sinusoïdale et de
l’onde
réfléchie
Ouvrir le fichier
( ondes stationnaires) et observer la corde soumise à la
superposition d’une onde progressive
sinusoïdale de fréquence f et de l’onde réfléchie sur un obstacle
fixe :
quelle est
sa forme ?
Elle
est sinusoïdale
L’onde obtenue est-elle
progressive ?
Non,
l’onde ne progresse
pas : elle est "stationnaire".
Quelle est l’influence de
la fréquence ?
Ceci
a lieu quelle
que soit la fréquence. (
animation)
L’onde stationnaire possède
des points immobiles (qui ne vibrent pas)
et d’autres vibrant avec une amplitude maximale. Les repérer sur la
simulation. Comment nomme-t-on ces points ?
Les
points immobiles
sont les nœuds
de vibration
Les points vibrant
avec une amplitude
maximale, sont des ventres
de vibration.
Remarque :
un nœud de vibration se trouve au niveau de l’obstacle fixe. Si
l’obstacle est libre, c’est un ventre qui se trouve au niveau de
l’obstacle.
Rappeler
la définition de la longueur d’onde l.
On
appelle longueur d'onde l
la distance séparant deux points
consécutifs du milieu de propagation vibrant en phase
Quelle relation lie la
longueur d’onde l
et la fréquence f de
l’onde ?

.
v étant la célérité de
l’onde
Quelle
est distance entre 2 nœuds ou 2 ventres consécutifs ?
2
ventres ou 2 noeuds consécutifs sont distants de

2.Réflexion
d’une onde sur 2 obstacles fixes
2.1. Propagation d’une onde non périodique entre 2
points fixes
L’onde
se réfléchit en O et en O’ . 
Au
bout de combien de temps Dt
l’onde redevient-elle identique à
elle-même ?
L’onde
fait un aller et retour
à la célérité v.
Donc
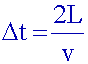
2.2. Propagation
d’une onde sinusoïdale entre 2 points fixes

Dans le cas général, l’onde, de
période
T,
doublement réfléchie
est-elle identique à l’onde incidente ? Quel est alors
l’aspect de la corde ?
Dans
le cas
général, l’onde doublement réfléchie n’est pas identique à l’onde
incidente. Donc un grand nombre d’ondes se superposent et la corde a un
aspect brouillé et instable.
A quelle condition l’onde,
de période T, doublement réfléchie est-elle
identique à l’onde incidente ?
Il
faut que Dt soit
un multiple de T, soit : Dt
= k T.
En
déduire une relation entre la longueur L de la corde et la longueur
d’onde
l.
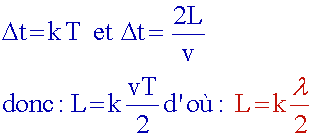
A quelle condition
obtient-on une onde stationnaire entre les 2 points
fixes ?
Une
onde stationnaire n’est
possible entre 2 points fixes que si la distance entre
ces points est
multiple
de la demi longueur d’onde; les 2 points fixes sont des
nœuds de
vibration.
Quelles
fréquences permettent l’obtention d’une onde
stationnaire ?
Donc
on n’obtient des ondes stationnaires
que pour les fréquences
f
k telles
que :

(
on retrouve la quantification des fréquences)
Conclure.
Si
une
corde, fixée à ses 2 extrêmités, est excitée sinusoïdalement
à une fréquence f, il n'apparaît une
onde stationnaire que si f est égale à une fréquence propre f
k
de vibration.
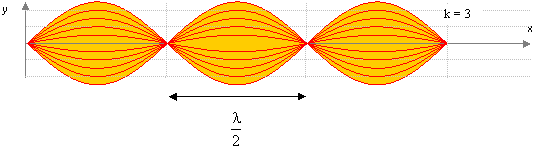
Les
extrémités de la
corde sont des nœuds de vibration.
Il se forme k fuseaux de
longueur

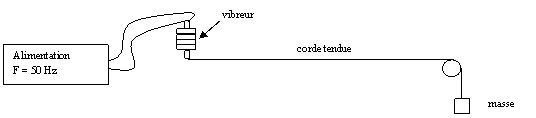
3. Etude
expérimentale d'ondes stationnaires
Le
but de ce paragraphe est de vérifier expérimentalement la
relation (1) :
v
est la vitesse de propagation de l’onde : elle ne
dépend que du milieu de propagation.
3.1 Ondes stationnaires le long d’une corde tendue entre 2
points fixes
Dans cette expérience, fk
est fixée (
c’est la fréquence du
vibreur ) et on fait varier L (longueur de la corde).
1) Caractéristiques
de
l’onde stationnaire
Placer une masse marquée m de
20
g à l'extrémité de la
corde.
Faire varier la longueur L de la corde en déplaçant un
support afin d'obtenir k =1 fuseau.
En déduire la valeur de l .
En déduire la valeur de v. ( f= 50 Hz)
Recommencer avec un
nombre de fuseaux k= 2 ….
| nombre
de fuseaux k |
1
|
2
|
3
|
4
|
| longueur
de corde L (cm) |
35
|
70
|
105
|
135
|
| l (cm) |
70
|
70
|
70
|
67.5
|
| v
(m/s-1) |
35
|
35
|
35
|
33.7
|
Qu’observe-t-on ?
v est constante. C'est
normal car elle ne dépend que du
milieu ( corde)
l
est
constante également.
Ces 2 grandeurs sont caractéristiques
de
l'onde stationnaire.
Conclure.
La
vitesse v a été calculée à l'aide de la relation (1) qui est bien
vérifiée.
2) Influence
des paramètres du dispositif sur le nombre k de fuseaux
La
célérité v de l’onde qui se propage le long d'une corde est liée à sa
tension F
et à sa masse linéique µ: 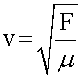 relation (2)
relation (2)
(la tension F est déterminée par la
valeur de la
masse m accrochée à la corde.)
Quels
paramètres peut-on faire varier (la fréquence étant fixée à f
= 50 Hz)?
On peut faire
varier la longueur L , la tension F et la masse
linéique µ de la corde.
1er
paramètre : longueur de la corde
que peut-on déduire du tableau
précédent
pour l et
m
constants ?
si
l
est constant, on voit que
plus L est grand, plus le nombre de
fuseaux k est important
(cela correspond bien à la relation
(1):

)
2ème
paramètre : tension F de la corde
Prendre
comme longueur de corde
la longueur L trouvée
dans le tableau précédent pour m = 20g et 2 fuseaux.
Faire
varier la valeur de la masse m et conserver L
constante. Noter le nombre de fuseaux obtenus.
| L
(cm) |
70
|
| m
(g) |
80
|
20
|
10
|
5
|
| k
|
1
|
2
|
3
|
4
|

|
8.9
|
8.9
|
9.5
|
8.9
|
D’après la
dernière ligne du tableau, on voit que la relation

= cste est ( aux erreurs de mesure près! ) vérifiée.
Cela
vérifie les relations (1) et (2), puisque :

3ème
paramètre : masse linéique µ de la corde
L’expérience est réalisée au
bureau du professeur avec 2 cordes, l’une de masse linéique µ et
l’autre de
masse linéique µ’, avec µ’ = 4 µ
La longueur de la corde étant
fixée à environ L = 1 m, la masse suspendue étant m = 200g
Que se passe-t-il si la corde est
remplacée
par celle de masse linéique
µ’, tout en conservant L, m, f ?
Avec
la corde de masse linéique µ’ = 4 µ, on observe 2 fuseaux.
Avec
la corde de masse linéique µ, on observe 1 fuseau.
Encore une
fois, ceci vérifie la relation (1), car :
pour la corde de masse
linéïque µ
:
pour
la corde de masse linéïque
µ' :
3.2 Ondes
stationnaires dans une
colonne d’air
Le
but de ce paragraphe est de vérifier expérimentalement la
relation (1) :
v
est la vitesse de propagation de l’onde : elle ne
dépend que du milieu
k est le nombre de fuseaux
fk
est une préquence propre ( pour laquelle il y a onde stationnaire)
Le
micro est sensible à une pression.
1)
Etude expérimentale dans un tube ouvert aux 2 extrémités:
Placer
le micro à l’entrée du tube et rechercher, à l’oscilloscope, la
fréquence f
4 du quatrième harmonique.

On augmente progressivement
la fréquence et on contrôle à l'oscilloscope.
La première
fréquence pour laquelle on obtient une sinusoïde d'amplitude importante
est f1 ( fondamental)...en augmentant, on trouve
le quatrième harmonique: f4 = 588 Hz
vérifier que


La longueur du tube est

et la vitesse de propagation du son dans l'air est environ
340m.s
-1.
donc
:
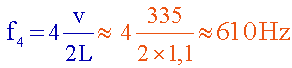
En
déplaçant le micro dans le tube, déterminer les positions des
ventres et des nœuds de pression.
Observation :
En
déplaçant le micro dans le tube, on constate que l’amplitude du signal
présente des maxima et des minima. Or, le micro
est sensible à une
pression.
Les
extrêmités ouvertes sont des noeuds de pression.
Remarque :
un noeud
de pression correspond à un ventre de vibration et réciproquement
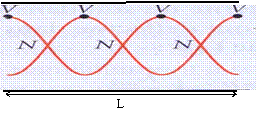
(voir
animation
sur un tuyau sonore)
( dans le schéma ci-contre, sont représentés les noeuds et ventres de vibration)
Pour
un mode propre de fréquence f
k, la longueur du
tube est
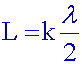
En déduire la valeur de la longueur
d’onde l.
Distance entre 2 ventres consécutifs
: 34
cm
Donc la longueur d'onde : l=
2×
34 = 68 cm
Lorsqu’une
colonne d’air vibre selon l’un de ses
modes propres, elle
est le siège d’une onde stationnaire présentant une alternance de nœuds
et de ventres de pression.
2 ventres (ou nœuds)
consécutifs sont séparés d’une distance de

2) Cas d’un
tube fermé à l’une de ses extrémités :
Un
ventre de vibration ( = un nœud de pression ) se trouve à l’extrémité
ouverte et un nœud de vibration à l’extrémité fermée.
Pour un mode propre de fréquence fk,
quelle est l’expression de la
longueur L du tube en fonction de k et l?
( dans le schéma ci-dessous, sont représentés les noeuds et ventres de vibration)
Ici on
a
l’amorce de
3 fuseaux ( f
3 ) : L =
2,5
l/2

De
façon
générale :
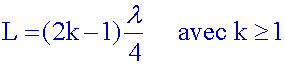
Quelle
est la valeur de la fréquence f1
du mode fondamental en
fonction de L?

or, d'après la
relation 1(

)
:

3)Tube
de Kundt :
(August Kundt, physicien allemand, 1839-1894)
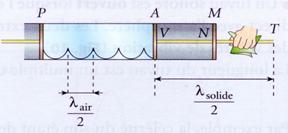
Dans
un tube transparent PA, on
dépose une poudre fine et légère.
Un
piston mobile P permet de
modifier la longueur de la colonne d’air du tube. Un piston en A,
obturant
pratiquement le tube sans toucher les parois, est placé de sorte que M
soit le
milieu de la tige métallique AT.
Par
frottement sur cette
dernière, on produit des ondes longitudinales progressives en déplaçant
légèrement ses extrémités. L’air est
mis en vibration par le piston A.
Un
système d'onde stationnaire
s'établit. La poudre est sensible à cette vibration et, lorsqu'on ne
frotte
plus la tige, on observe des petits tas de poudre (cela est réalisé en réglant
la position de P).
A
quoi est dû le son que l’on entend ?
Le
son
est produit par la vibration de l’air de la colonne comprise entre les
pistons A et P.
Que
matérialisent ces petits
tas de poudre ?
Ils
correspondent aux sections de la colonne d’air ne vibrant pas
c’est-à-dire à des nœuds de vibration (la poudre qui se trouve aux
ventres de vibration est projetée vers les nœuds où elle s’accumule).
Animation
: onde
sonore dans un tuyau d'orgue
 .
v étant la célérité de
l’onde
.
v étant la célérité de
l’onde  .
v étant la célérité de
l’onde
.
v étant la célérité de
l’onde 

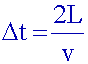

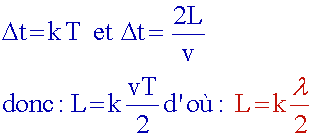
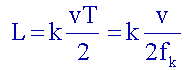



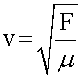
 )
) 
 = cste est ( aux erreurs de mesure près! ) vérifiée.
= cste est ( aux erreurs de mesure près! ) vérifiée.
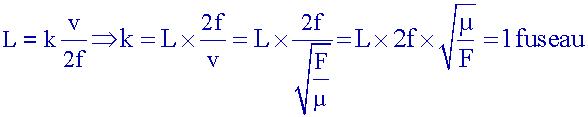
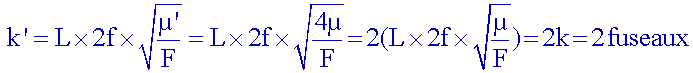




 et la vitesse de propagation du son dans l'air est environ
340m.s-1.
et la vitesse de propagation du son dans l'air est environ
340m.s-1.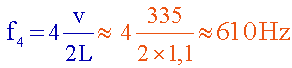

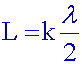


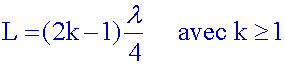

 )
:
)
: 

